ШРЕДЕРА УРАВНЕНИЕ, математич. соотношение, выражающее связь между растворимостью кристаллич. тела x_T при темп-ре T (в К), его теплотой плавления дh_nл (в кал/моль) и темп-рой плавления T_nл:

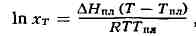
где R - газовая постоянная; дh_nл принимается постоянной в интервале Т_пл-T. Строгое применение Ш. у. ограничено идеальными растворами. Построив по Ш. у. кривые температурной зависимости растворимости для твёрдой фазы каждого из компонентов двойной системы, можно найти эвтектическую точку (см. Эвтектика) и получить растворимости диаграмму.

Ш. у. выведено в 1890 И. Ф. Шредером. Оно известно также под назв. "логарифмики Шредера" и уравнения Шредера - Ле Шателье (A. Лe Шателье ранее получил зависимость растворимости от темп-ры в дифференциальной форме, на основании к-рой в 1894 вывел уравнение, аналогичное Ш. у.).

Лит.: Кипнис А. Я., Развитие химической термодинамики в России, M.- Л., 1964. См. также лит. при ст. Растворы.

M. X. Карапетьянц.

ШРЁДЕР-ДЕВРИЕНТ (Schroder-Devrient, урожд. Шредер) Вильгельмина (6.12.1804, Гамбург, - 26.1.1860, Кобург), немецкая певица (сопрано). Пению училась у Ю. Моцатти в Вене. В 1821 дебютировала в партии Памины ("Волшебная флейта" Моцарта). Гастролировала в городах Италии, в Париже, Лондоне, Праге. Исполнила партию Леоноры ("Фиделио" Бетховена, 1822, Вена), к-рая принесла ей славу выдающейся певицы Европы. В 1823-47 солистка придворной оперы в Дрездене. За участие в Дрезденском восстании 1849 была выслана из Саксонии и не выступала до 1856. Гастролировала в России. В иск-ве Ш.-Д. сочеталось вокальное мастерство с большой драм. одарённостью. Среди лучших партий: Сента ("Летучий голландец" Вагнера), Агата ("Вольный стрелок" Вебера).

Лит.: Серов A. H., Критические статьи, т. 3, СПБ, 1893, с. 1361-75; Wоlzоgеn A. vоn, Wilhelmine Schröder-Devrient, Lpz., 1863; Hagemann K., Wilhelmine Schröder-Devrient, Wiesbaden, 1947.

ШРЁДИНГЕР (Schrodinger) Эрвин (12. 8.1887, Вена, - 4.1.1961, там же; похоронен в Альпбахе, Тироль), австрийский физик, один из создателей квантовой механики. Окончил Венский ун-т (1910). С 1911 работал в Физ. ин-те Венского ун-та. В 1920 проф. Высшей технич. школы в Штутгарте, в 1921-Высшей технич. школы в Бреслау (Вроцлаве), в 1921-27 - Высшей технической школы в Цюрихе, с 1927 проф. Берлинского ун-та. В 1933-35 профессор Оксфордского ун-та, в 1936-38 - ун-та в Граце, в 1938-39 - в Генте, с 1940 проф. Королевской академии в Дублине, затем директор основанного им Ин-та высших исследований. С 1956 проф. Венского ун-та. Осн. труды по математич. физике, теории относительности, физике атома и биофизике. К ранним работам Ш. относятся исследования по теории кристаллич. решётки и создание в 1920 математич. теории цвета, к-рая легла в основу совр. колориметрии. Важнейшей заслугой Ш. является создание им волновой механики (кон. 1925 - нач. 1926): исходя из гипотезы Л. де Бройля о волнах материи, он показал, что стационарные состояния атомных систем могут рассматриваться как собственные колебания волнового поля, соответствующего данной системе; Ш. нашёл осн. ур-ние нерелятивистской квантовой механики (Шрёдингера уравнение) и дал его решение для ряда частных задач, а также общий метод его применения в теории возмущений.

Э. Шрёдингер.

Установил связь волновой механики с "матричной механикой" В. Гейзенберга, M. Борна и П. Иордана и доказал их физ. тождественность. Развитый Ш. математич. формализм и введённая им волновая функция пси явились наиболее адекватным математич. аппаратом квантовой механики и её применений. Нобелевская пр. (1933). Иностр. чл. АН СССР (1934).

Соч.: Abhandlungen zur Wellenmechanik, 2 Aufl., Lpz., 1928; в рус. пер. - Избр. труды по квантовой механике, M., 1976 (сер. "Классики науки"); Что такое жизнь? С точки зрения физика, 2 изд., M., 1972.

Л. С. Поляк.

ШРЁДИНГЕРА УРАВНЕНИЕ, осн. динамич. уравнение нерелятивистской квантовой механики; названо в честь австр. физика Э. Шрёдингера, к-рый предложил его в 1926. В квантовой механике Ш. у. играет такую же фундаментальную роль, как уравнение движения Ньютона в классич. механике и Максвелла уравнения в классич. теории электромагнетизма. Ш. у. описывает изменение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая функция Y в начальный момент времени, то, решал Ш. у., можно найти Y в любой последующий момент времени t.

Для частицы массы т, движущейся под действием силы, порождаемой потенциалом V (х, у, Z, t), Ш. у. имеет вид:

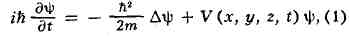
где i = -(1)^1/2 , h = 1,05х10^-27 эрг-сек - Планка постоянная,

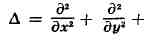
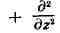
- Лапласа оператор (х, у, z-координаты), Это уравнение наз. временным Ш. у. Если потенциал V не зависит от времени, то решения Ш. у. можно представить в виде:

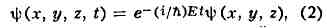
где E - полная энергия квантовой системы, а пси(х, у, z) удовлетворяет стационарному Ш. у.:

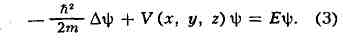
Для квантовых систем, движение к-рых происходит в огранич. области пространства, решения Ш. у. существуют только для нек-рых дискретных значений энергии: E₁, E₂, ..., Е_п,···; члены этого ряда (в общем случае бесконечного) нумеруются набором целых квантовых чисел п. Каждому значению E_nсоответствует волновая функция пси_n (x, у, z), и знание полного набора этих функций позволяет вычислить все измеримые характеристики квантовой системы.В важном частном случае кулоновского потенциала

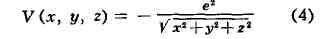
(где е - элементарный электрич. заряд) Т. у. описывает атом водорода, и E_n представляют собой энергии стационарных состояний атома.

Ш. у. является математич. выражением фундаментального свойства микрочастиц - корпускулярно-волнового дуализма, согласно к-рому все существующие в природе частицы материи наделены также волновыми свойствами (эта гипотеза впервые была высказана Л. де Бройлем в 1924). Ш. у. удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, содержит описание движения частиц по законам классич. механики. Переход от Ш. у. к классич. траекториям подобен переходу от волновой оптики к геометрической. Аналогия между классич. механикой и геометрич. оптикой, к-рая является предельным случаем волновой, сыграла важную роль в установлении Ш. у.

С математич. точки зрения Ш. у. есть волновое уравнение и по своей структуре подобно уравнению, описывающему колебания нагруженной струны. Однако, в отличие от решений уравнения колебаний струны, к-рые дают геометрич. форму струны в данный момент времени, решения пси (x, у, z, t) Ш. у. прямого физ. смысла не имеют. Смысл имеет квадрат волновой функции, а именно величина p_n (х, у, z,t) =| пси_n (х, y, z, t)|², равная вероятности нахождения частицы (системы) в момент ( в квантовом состоянии и в точке пространства с координатами х, у, z. Эта вероятностная интерпретация волновой функции - один из осн. постулатов квантовой механики.

Математич. формулировка постулатов квантовой механики, основанная на Ш. у., носит название волновой механики. Она полностью эквивалентна т. н. матричной механике В. Гейзенберга, к-рая была сформулирована им в 1925.

Ш. у. позволяет объяснить и предсказать большое число явлений атомной физики, а также вычислить осн. характеристики атомных систем, наблюдаемые на опыте, напр., уровни энергии атомов, изменение спектров атомов под влиянием электрич. и магнитного полей и т. д. С помощью Ш. у. удалось также понять и количественно описать широкий круг явлений ядерной физики, напр., закономерности a-распада, y-излучение ядер, рассеяние нейтронов на ядрах и др.

Лит.: Шрёдингер Э., Новые пути в физике. Статьи и речи, M., 1971. См. также лит. к ст. Квантовая механика.

Л. И. Пономарёв.